ZeroJudge I859: Can You Solve It?

題目敘述

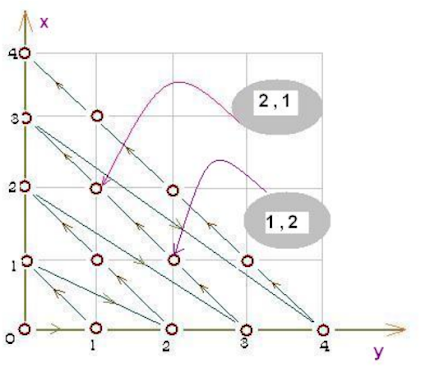
每筆測資第一行有一個正整數N，接下來會有N行，每行會有四個正整數，分別代表起點和終點的x和y座標。根據笛卡爾坐標系，需要按照以下所示的箭頭路徑從一個圓圈移動到另一個圓圈。
例如，要從 (0, 3) 到 (3, 0)，您必須經過兩個中間圓 (1, 2) 和 (2, 1)。 所以，在這種情況下，所需的總步數是 2 + 1 = 3。

要求輸出從起點走到終點需要走幾步。

範例輸入 #1

3

0 0 0 1

0 0 1 0

0 0 0 2

範例輸出 #1

Case 1: 1

Case 2: 2

Case 3: 3

解題思路

如果把步數標出來的話，可以發現Y軸 (橫軸) 的步數是 0 --> 1 --> 3 --> 5 --> 9，以此類推。舉例來說，當x+y等於2的時候，可以發現這些點都落在 (0, 2) 這個點的斜線上，更可以發現 (1, 1) 這個點是 (0, 2) 的步數＋1，也就是其x座標。同理，(2, 0) 的步數就是 (0, 2) 的步數＋2。

可以先設定一個陣列，並將 0、1、3、6、10．．．等數字存放到Y座標 (橫軸) 的位置上。收資料的時候判斷x+y是多少就找這個位置的步數然後加上x座標的值。

解題程式碼如下 (僅供參考)：

#include <iostream>
#include <vector>
using namespace std;

int main() {
    cin.sync_with_stdio(0);
    cin.tie(0);
    vector<long long int>Chueh;
    long long int count = 0, add = 0;
    for (int i = 0; i<=200000; i++)
    {
        count += add;
        Chueh.push_back(count);
        add++;
    }
    int N;
    cin >> N;
    for (int i = 0; i<N; i++)
    {
        long long int a, b;
        cin >> a >> b;
        long long int start = Chueh[a+b] + a;
        cin >> a >> b;
        long long int finish = Chueh[a+b] + a;
        cout << "Case " << i+1 << ": " << finish-start << "\n";
    }
}