ZeroJudge H206: 強者就是要戰，但......什麼才是強者呢？

題目敘述

每筆資料第一行有一個正整數N，下一行會有N個整數。要求輸出此數列中的「最強者」。

最強者定義：

假設現在有 N 人，我們可以分為左半邊 N/2 人和右半邊 N/2 人。

同樣地，對於左半邊 N/2 人，可以繼續平分為 N/4 人和 N/4 人，

直到無法再平分，也就是只剩下 1 人為止。

對於只有 1 人的區間，那人當然就是該區間內的最強者。

對於其他區間，則在找到左半邊最強者和右半邊最強者後，就可以簡單地對兩數字比較，以得到本身區間最強者。

但是強者的定義時常在變化，有時以小博大，有時以大搏小，兩者交替出現。

也就是假設這回合大者優先，則下回合會是小者優先，下下回合則又回到大者優先，依序下去......

這邊我們預設最初 N 人的區間為大者優先，

因此所劃分出的 N/2, N/2 區間將為小者優先，繼續劃分出的 N/4, N/4, N/4, N/4 則又回到大者優先......

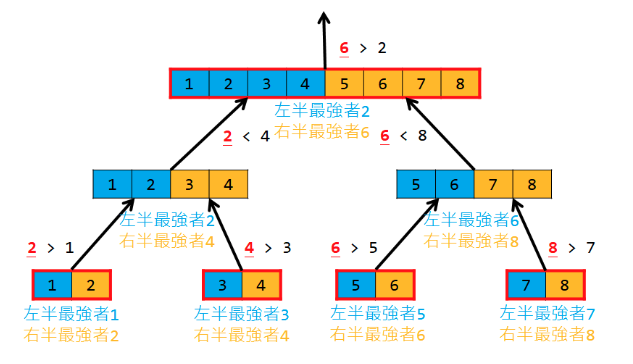
範例圖：

範例輸入 #1

8

1 2 3 4 5 6 7 8

範例輸出 #1

6

解題思路

使用遞迴的方式將數量一直切成一半，當數列只剩下一個數字時 (左界線＝右界線)，就return 目前的數字。大小的判斷可以每次進入函式時將一個布林值反轉並且return 最大值或最小值。

解題程式碼如下 (僅供參考)：

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

vector<int>num;

int findMax (int l, int r, bool bigFirst)
{
    if (l == r)
    {
        return num[l];
    }
    if (bigFirst)
    {
        int hi = max(findMax(l, (l+r)/2, false), findMax(((l+r)/2)+1, r, false));
        return hi;
    }
    int hi = min(findMax(l, (l+r)/2, true), findMax(((l+r)/2)+1, r, true));
    return hi;
}

int main() {
    cin.sync_with_stdio(0);
    cin.tie(0);
    int N;
    cin >> N;
    for (int i = 0; i<N; i++)
    {
        int tmp;
        cin >> tmp;
        num.push_back(tmp);
    }
    cout << findMax(0, int(num.size())-1, true) << "\n";
}